In the given figure, 0 is the center of a circle, BOA is its diameter and the tangent at the point P meets BA extended at T. If ∠PBO = 30° then ∠PTA = ?

Question

In the given figure, 0 is the center of a circle, BOA is its diameter and the tangent at the point P meets BA extended at T. If ∠ PBO = 30° then ∠ PTA = ?

Philoid · Accepted Answer

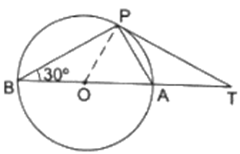
In △BOP

OB = OP [radii of same circle]

∠OPB = ∠PBO

[Angles opposite to equal sides are equal]

As, ∠PBO = 30°

∠OPB = 30°

Now,

∠OPT = 90°

[Tangents drawn at a point on circle is perpendicular to the radius through point of contact]

∠BPT = ∠OPB + ∠OPT = 30° + 90° = 120°

Now, In ΔBPT

∠BPT + ∠PBO + ∠PTB = 180°

120° + 30° + ∠PTB = 180°

∠PTB = 30°

∠PTA = ∠PTB = 30°