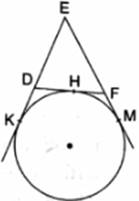
Given : In the given figure, a circle touches the side DF of ΔEDF at H and touches ED and EF produced at K and M respectively and EK = 9 cm

To Find : Perimeter of △EDF

As we know that, Tangents drawn from an external point to a circle are equal.

So, we have

KD = DH …[1]

[Tangents from point D]

HF = FM …[2]

[Tangents from point F]

Now Perimeter of Triangle PCD

= ED + DF + EF

= ED + DH + HF + EF

= ED + KD + FM + EF [From 1 and 2]

= EK + EM

Now,

EK = EM = 9 cm as tangents drawn from an external point to a circle are equal

So, we have

Perimeter = EK + EM = 9 + 9 = 18 cm