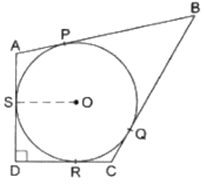
In quadrilateral ORDS

∠ORD = 90°

[∵ Tangent at any point on the circle is perpendicular to the radius through point of contact]

∠OSD = 90°

[∵ Tangent at any point on the circle is perpendicular to the radius through point of contact]

∠SDR = 90° [AD ⏊ CD]

By angle sum property of quadrilateral PQOB

∠ORD + ∠OSD + ∠SDR + ∠SOR = 360°

90° + 90° + 90° + ∠SOR = 360°

∠SOR = 90°

As all angles of this quadrilaterals are 90° The quadrilateral is a rectangle

Also, OS = OR = r

i.e. adjacent sides are equal, and we know that a rectangle with adjacent sides equal is a square

∴ POQB is a square

And OS = OR = DR = DS = r = 10 cm [1]

Now,

As we know that tangents drawn from an external point to a circle are equal

In given figure, We have

CQ = CR …[2]

[∵ tangents from point C]

PB = BQ = 27 cm

[∵Tangents from point B and PB = 27 cm is given]

BC = 38 cm [Given]

BQ + CQ = 38

27 + CQ = 38

CQ = 11 cm

From [2]

CQ = CR = 11 cm

Now,

CD = CR + DR

CD = 11 + 10 = 21 cm [from 1, DR = 10 cm]