In the given figure, O is the center of two concentric circles of radii 5 cm and 3 cm. From an external point P tangents PA and PB are drawn to these circles. If PA = 12 cm then PB is equal to
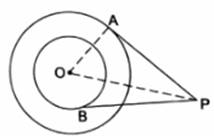
In given Figure,
OA ⏊ AP [Tangent at any point on the circle is perpendicular to the radius through point of contact]
∴ In right - angled △OAP,
By Pythagoras Theorem
[i.e. (hypotenuse)2 = (perpendicular)2 + (base)2]
(OP)2 = (OA)2 + (PA)2
Given, PA = 12 cm and OA = radius of outer circle = 5 cm
(OP)2 = (5)2 + (12)2
(OP)2 = 25 + 144 = 136
OP = 13 cm …[1]
Also,
OB ⏊ BP [Tangent at any point on the circle is perpendicular to the radius through point of contact]
∴ In right - angled △OBP,
By Pythagoras Theorem
[i.e. (hypotenuse)2 = (perpendicular)2 + (base)2 ]
(OP)2 = (OB)2 + (PB)2
Now, OB = radius of inner circle = 3 cm
And, from [2] (OP) = 13 cm
(13)2 = (3)2 + (PB)2
(PB)2 = 169 - 9 = 160
PB = 4√10 cm