In the given figure, O is the center of a circle, PQ is a chord and the tangent PT at P makes an angle of 50° with PQ. Then, ∠POQ = ?

Question

In the given figure, O is the center of a circle, PQ is a chord and the tangent PT at P makes an angle of 50° with PQ. Then, ∠ POQ = ?

Philoid · Accepted Answer

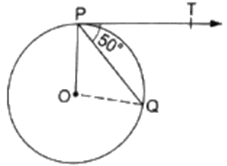
In the given figure PT is a tangent to circle ∴ we have

∠OPT = 90°

[Tangents drawn at a point on circle is perpendicular to the radius through point of contact]

∠OPQ + ∠QPT = 90°

∠OPQ + 50° = 90°

∠OPQ = 40°

Now, In △POQ

OP = OQ

∠PQO = ∠QPO = 40°

[Angles opposite to equal sides are equal]

Now,

∠ PQO + ∠QPO + ∠ POQ = 180° [

By angle sum property of triangle]

40° + 40° + ∠POQ = 180°

∠POQ = 100°