RS Aggarwal - Mathematics

Book: RS Aggarwal - Mathematics

Chapter: 12. Circles

Subject: Maths - Class 10th

Q. No. 6 of Formative Assessment (Unit Test)

Listen NCERT Audio Books to boost your productivity and retention power by 2X.

6

In the given figure, PA and PB are the tangents to a circle with center O. Show that the points A, 0, B, P are concyclic.

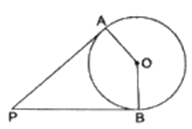
Given : PA and PB are tangents to a circle with center O


To show : A, O, B and P are concyclic i.e. they lie on a circle i.e. AOBP is a cyclic quadrilateral.


Proof :


OB ⏊ PB and OA ⏊ AP


[Tangent at any point on the circle is perpendicular to the radius through point of contact]


∠OBP = ∠OAP = 90°


∠OBP + ∠OAP = 90 + 90 = 180°


AOBP is a cyclic quadrilateral i.e. A, O, B and P are concyclic.


[ As we know if the sum of opposite angles in a quadrilateral is 180° then quadrilateral is cyclic ]


Hence Proved.


Chapter Exercises

Exercise 12A
Exercise 12B
Multiple Choice Questions (MCQ)
Formative Assessment (Unit Test)

More Exercise Questions

1

In the given figure, O is the center of a circle, PQ is a chord and the tangent PT at P makes an angle of 50° with PQ. Then, ∠POQ = ?
2

If the angle between two radii of a circle is 130° then the angle between the tangents at the ends of the radii is
3

If tangents PA and PB from a point P to a circle with center O are drawn so that ∠APB = 80° then ∠POA = ?
4

In the given figure, AD and AE are the tangents to a circle with center O and BC touches the circle at F. If AE = 5 cm then perimeter of ΔABC is
5

In the given figure, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively.

If AB = x cm, BC = 7 cm, CR = 3 cm and


AS = 5 cm, find x.
6

In the given figure, PA and PB are the tangents to a circle with center O. Show that the points A, 0, B, P are concyclic.
7

In the given figure, PA and PB are two tangents from an external point P to a circle with center O. If ∠PBA = 65°, find ∠OAB and ∠APB.
8

Two tangent segments BC and BD are drawn to a circle with center O such that ∠CBD = 120°. Prove that OB = 2BC.
9

Fill in the blanks.

(i) A line intersecting a circle in two distinct points is called a ……..


(ii) A circle can have ………..parallel tangents at the most.


(iii) The common point of a tangent to a circle and the circle is called the ………..


(iv) A circle can have ………..tangents.
10

Prove that the lengths of two tangents drawn from an external point to a circle are equal.
11

Prove that the tangents drawn at the ends of the diameter of a circle are parallel.
12

In the given figure, if AB = AC, prove that BE = CE.
13

If two tangents are drawn to a circle from an external point, show that they subtend equal angles at the center.
14

Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
15

Prove that the parallelogram circumscribing a circle, is a rhombus.
16

Two concentric circles are of radii 5 cm and 3 cm respectively. Find the length of the chord of the larger circle which touches the smaller circle.
17

A quadrilateral is drawn to circumscribe a circle. Prove that the sums of opposite sides are equal.
18

Prove that the opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the center of the circle.
19

Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact at the center.
20

PQ is a chord of length 16 cm of a circle of radius 10 cm. The tangents at P and Q intersect at a point T as shown in the figure.

Find the length of TP.

Students Store