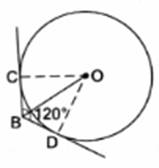
Given : A circle with center O , BC and BD are two tangents such that ∠CBD = 120°

To Proof : OB = 2BC

Proof :

In △BOC and △BOD

BC = BD

[Tangents drawn from an external point are equal]

OB = OB

[Common]

OC = OD

[Radii of same circle]

△BOC ≅ △BOD [By Side - Side - Side criterion]

∠OBC = ∠OBD

[Corresponding parts of congruent triangles are congruent]

∠OBC + ∠OBD = ∠CBD

∠OBC + ∠OBC = 120°

2 ∠OBC = 120°

∠OBC = 60°

In △OBC

⇒OB = 2BC

Hence Proved !