RS Aggarwal - Mathematics

Book: RS Aggarwal - Mathematics

Chapter: 12. Circles

Subject: Maths - Class 10th

Q. No. 10 of Formative Assessment (Unit Test)

Listen NCERT Audio Books to boost your productivity and retention power by 2X.

10

Prove that the lengths of two tangents drawn from an external point to a circle are equal.

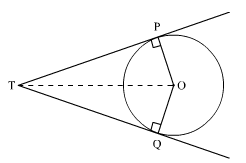
Let us consider a circle with center O.


TP and TQ are two tangents from point T to the circle.


To Proof : PT = QT


Proof :


OP ⏊ PT and OQ ⏊ QT


[Tangents drawn at a point on circle is perpendicular to the radius through point of contact]


∠OPT = ∠OQT = 90°


In △TOP and △QOT


∠OPT = ∠OQT


[Both 90°]


OP = OQ


[Common]


OT = OT


[Radii of same circle]


△TOP ≅ △QOT


[By Right Angle - Hypotenuse - Side criterion]


PT = QT


[Corresponding parts of congruent triangles are congruent]


Hence Proved.


Chapter Exercises

Exercise 12A
Exercise 12B
Multiple Choice Questions (MCQ)
Formative Assessment (Unit Test)

More Exercise Questions

1

In the given figure, O is the center of a circle, PQ is a chord and the tangent PT at P makes an angle of 50° with PQ. Then, ∠POQ = ?
2

If the angle between two radii of a circle is 130° then the angle between the tangents at the ends of the radii is
3

If tangents PA and PB from a point P to a circle with center O are drawn so that ∠APB = 80° then ∠POA = ?
4

In the given figure, AD and AE are the tangents to a circle with center O and BC touches the circle at F. If AE = 5 cm then perimeter of ΔABC is
5

In the given figure, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively.

If AB = x cm, BC = 7 cm, CR = 3 cm and


AS = 5 cm, find x.
6

In the given figure, PA and PB are the tangents to a circle with center O. Show that the points A, 0, B, P are concyclic.
7

In the given figure, PA and PB are two tangents from an external point P to a circle with center O. If ∠PBA = 65°, find ∠OAB and ∠APB.
8

Two tangent segments BC and BD are drawn to a circle with center O such that ∠CBD = 120°. Prove that OB = 2BC.
9

Fill in the blanks.

(i) A line intersecting a circle in two distinct points is called a ……..


(ii) A circle can have ………..parallel tangents at the most.


(iii) The common point of a tangent to a circle and the circle is called the ………..


(iv) A circle can have ………..tangents.
10

Prove that the lengths of two tangents drawn from an external point to a circle are equal.
11

Prove that the tangents drawn at the ends of the diameter of a circle are parallel.
12

In the given figure, if AB = AC, prove that BE = CE.
13

If two tangents are drawn to a circle from an external point, show that they subtend equal angles at the center.
14

Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
15

Prove that the parallelogram circumscribing a circle, is a rhombus.
16

Two concentric circles are of radii 5 cm and 3 cm respectively. Find the length of the chord of the larger circle which touches the smaller circle.
17

A quadrilateral is drawn to circumscribe a circle. Prove that the sums of opposite sides are equal.
18

Prove that the opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the center of the circle.
19

Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact at the center.
20

PQ is a chord of length 16 cm of a circle of radius 10 cm. The tangents at P and Q intersect at a point T as shown in the figure.

Find the length of TP.

Students Store