Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.

Question

Philoid · Accepted Answer

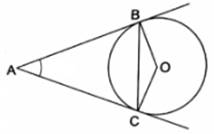
Let us consider a circle with center O and BC be a chord, and AB and AC are tangents drawn at end of a chord

To Prove : AB and AC make equal angles with chord, i.e. ∠ABC = ∠ACB

Proof :

In △ABC

AB = PC

[Tangents drawn from an external point to a circle are equal]

∠ACB = ∠ABC

[Angles opposite to equal sides are equal]

Hence Proved.