Prove that the parallelogram circumscribing a circle, is a rhombus.
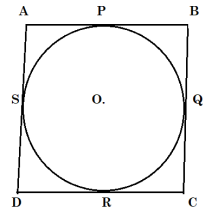
Consider a circle circumscribed by a parallelogram ABCD, Let side AB, BC, CD and AD touch circles at P, Q, R and S respectively.
To Proof : ABCD is a rhombus.
As ABCD is a parallelogram
AB = CD and BC = AD …[1]
[opposite sides of a parallelogram are equal]
Now, As tangents drawn from an external point are equal.
We have
AP = AS
[tangents from point A]
BP = BQ
[tangents from point B]
CR = CQ
[tangents from point C]
DR = DS
[tangents from point D]
Add the above equations
AP + BP + CR + DR = AS + BQ + CQ + DS
AB + CD = AS + DS + BQ + CQ
AB + CD = AD + BC
AB + AB = BC + BC [From 1]
AB = BC …[2]
From [1] and [2]
AB = BC = CD = AD
And we know,
A parallelogram with all sides equal is a rhombus
So, ABCD is a rhombus.
Hence Proved.