Book: RS Aggarwal - Mathematics
Chapter: 12. Circles
Subject: Maths - Class 10th
Q. No. 18 of Formative Assessment (Unit Test)
Listen NCERT Audio Books to boost your productivity and retention power by 2X.
Prove that the opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the center of the circle.
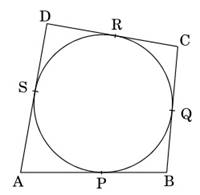
Consider a quadrilateral, ABCD circumscribing a circle with center O and AB, BC, CD and AD touch the circles at point P, Q, R and S respectively.
Joined OP, OQ, OR and OS and renamed the angles (as in diagram)
To Prove : Opposite sides subtends supplementary angles at center i.e.
∠AOB + ∠COD = 180° and ∠BOC + ∠AOD = 180°
Proof :
In △AOP and △AOS
AP = AS
[Tangents drawn from an external point are equal]
AO = AO
[Common]
OP = OS
[Radii of same circle]
△AOP ≅ △AOS
[By Side - Side - Side Criterion]
∠AOP = ∠AOS
[Corresponding parts of congruent triangles are congruent]
∠1 = ∠2 …[1]
Similarly, We can Prove
∠3 = ∠4 ….[2]
∠5 = ∠6 ….[3]
∠7 = ∠8 ….[4]
Now,
As the angle around a point is 360°
∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°
∠2 + ∠2 + ∠3 + ∠3 + ∠6 + ∠6 + ∠7 + ∠7 = 360° [From 1, 2, 3 and 4]
2(∠2 + ∠3 + ∠6 + ∠7) = 360°
∠AOB + ∠COD = 180°
[As, ∠2 + ∠3 = ∠AOB and ∠5 + ∠6 = ∠COD] [5]
Also,
∠AOB + ∠BOC + ∠COD + ∠AOD = 360°
[Angle around a point is 360°]
∠AOB + ∠COD + ∠BOC + ∠AOD = 360°
180° + ∠BOC + ∠AOD = 360° [From 5]
∠BOC + ∠AOD = 180°
Hence Proved
