Let us assume f (x) = x⁴ + x³ ‒ 23x² ‒ 3x + 60

As √3 and –√3 are the zeros of the given polynomial therefore each one of (x - √3) and (x - √3) is a factor of f (x)

Consequently, (x – √3) (x + √3) = (x² – 3) is a factor of f(x)

Now, on dividing f (x) by (x² – 3) we get:

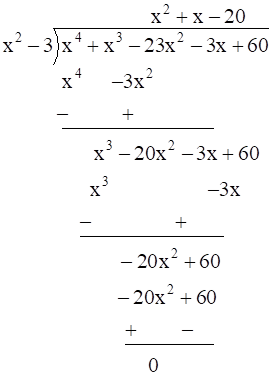
f (x) = 0

(x² + x – 20) (x² – 3) = 0

(x² + 5x – 4x – 20) (x² – 3)

[x (x + 5) – 4 (x + 5)] (x² – 3)

(x – 4) (x + 5) (x – ) (x + ) = 0

∴ x = 4 or x = - 5 or x = or x = -

Hence, all the zeros of the given polynomial are , -, 4 and - 5