Find all the zeros of the polynomial (2x4 ‒ 11x3 + 7x2 + 13x ‒ 7), it being given that two of its zeros are (3 + √3) and (3 ‒ √3)
Let us assume f (x) = 2x4 – 11x3 + 7x2 + 13x - 7
As (3 + √2) and (3- √2) are the zeros of the given polynomial therefore each one of (x + 3 + √2) and (x + 3 - √2) is a factor of f (x)
Consequently, [(x – (3 + √2)][(x – (3 -√2)
= [(x – 3) -√2] [(x – 3) + ![]() ]
]
= [(x – 3)2 – 2] = x2 – 6x + 7 is a factor of f (x)
Now, on dividing f (x) by (x2 – 6x + 7) we get:
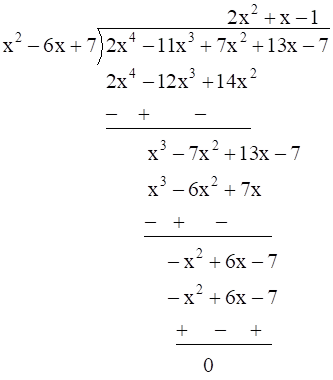
f (x) = 0
2x4 - 11x3 + 7x2 + 13x – 7 = 0
(x2 - 6x + 7) (2x2 + x – 7) = 0
(x + 3 + √2) (x + 3 -√2) (2x – 1) (x + 1) = 0
∴ x = - 3 - √2 or x = - 3 + √2 or x = 1/2 or x = - 1
Hence, all the zeros of the given polynomial are (-3 -√2), (-3 + √2), 1/2 and – 1
19