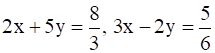
We have,

…eq.1

…eq.2

Let us first simplify eq.1 & eq.2 by taking LCM of denominators,

Eq.1

⇒ 6x + 15y = 8 …eq.3

Eq.2

⇒ 18x – 12y = 5 …eq 4

To solve these equations, we need to make one of the variables (in both the equations) have same coefficient.

Lets multiply eq.3 by 18 and eq.4 by 6, so that variable x in both the equations have same coefficient.

Recalling equations 3 & 4,

6x + 15y = 8 [×18]

18x – 12y = 5 [×6]

⇒ 108x + 270y = 144

108x – 72y = 30

On solving these two equations we get,

⇒ 342y = 114

⇒

⇒

Substitute in eq.3/eq.4, as per convenience of solving.

Thus, substituting in eq.3, we get

6x + = 8

⇒ 6x + 5 = 8

⇒ 6x = 8 – 5

⇒ 6x = 3

⇒

Hence, we have and