We have,

a²x + b²y = c² …(i)

b²x + a²y = d²…(ii)

To solve these equations, we need to simplify them.

So, by adding equations (i) and (ii), we get

(a²x + b²y) + (b²x + a²y) = c² + d²

⇒ (a²x + b²x) + (b²y + a²y) = c² + d²

⇒ (a² + b²)x + (a² + b²)y = c² + d²

Now dividing it by (a² + b²), we get

x + y = (c² + d²)/( a² + b²) …(iii)

Similarly, subtracting equations (i) and (ii),

(a²x + b²y) – (b²x + a²y) = c² – d²

⇒ (a²x – b²x) – (b²y – a²y) = c² – d²

⇒ (a² – b²)x – (a² – b²)y = c² – d²

Dividing the equation by (a² – b²), we get

x – y = (c² – d²)/ (a² – b²) …(iv)

To solve equations (iii) and (iv), we need to make one of the variables (in both the equations) have same coefficient.

Here the variables x in both the equations have same coefficients.

⇒

⇒

⇒

⇒

⇒

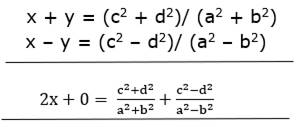
Substitute in eq.(iii)/eq.(iv), as per convenience of solving.

Thus, substituting in eq.(iii), we get

⇒

⇒

⇒

⇒

Hence, we have and .