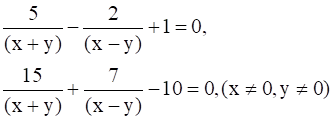
We have,

…(i)

…(ii)

Let 1/(x + y) = p and 1/(x - y) = q. Now,

From equation (i), 5p – 2q + 1 = 0 …(iii)

From equation (ii), 15p + 7q – 10 = 0 …(iv)

From equation (iii), we get a₁ = 5, b₁ = - 2 and c₁ = 1

And from equation (iv), we get a₂ = 15, b₂ = 7 and c₂ = - 10

Using cross multiplication,

⇒

⇒

⇒

⇒ and

⇒ and

⇒ p = 1/5 and q = 1

⇒ and [∵ p = 1/(x + y) and q = 1/(x - y)]

To solve these, we need to take reciprocal of these equations. By taking reciprocal, we get

x + y = 5 and x – y = 1

Rearranging them again,

x + y – 5 = 0 …(v)

x – y – 1 = 0 …(vi)

From equation (v), we get a₁ = 1, b₁ = 1 and c₁ = - 5

And from equation (vi), we get a₂ = 1, b₂ = - 1 and c₂ = - 1

Using cross multiplication,

⇒

⇒

⇒

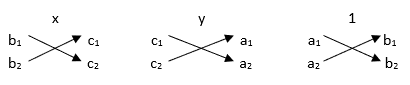
⇒ and

⇒ and

⇒ x = 3 and y = 2

Thus, x = 3, y = 2