The plates of a parallel plate capacitor have an area of 90 cm2 each and are separated by 2.5 mm. The capacitor is charged by connecting it to a 400V supply.

(a) How much electrostatic energy is stored by the capacitor?


(b) View this energy as stored in the electrostatic field between the plates, and obtain the energy per unit volume u. Hence arrive at a relation between u and the magnitude of electric field E between the plates.

Area of the plates of a parallel capacitor (A) = 90cm2 = 910-3m

Distance between the plates (d) = 2.5mm = 2.510-3m


Potential difference across the plates (V) = 400V


(a) Electrostatic energy stored in the capacitor(E) = CV2


Since, Capacitance (C) =


∴


Where, = Absolute Permittivity of free space = 8.8510-12C2N-1m-2



⇒ E = 2.5510-6J


The electrostatic energy stored by the capacitor = 2.5510-6J


(b) Volume between plates of capacitor (v) = A × d


= 910-3m2 × 2.510-3m


= 2.2510-5m3


Therefore, Energy per unit volume (u) = E/v




The energy per unit volume (u) = 0.113 Jm-3


Relation between u and the magnitude of electric field E between the plates


Since,


Energy per unit volume (u) = E/v


= CV2 /v


Here, V = voltage across capacitor


v = volume between plates of capacitor,




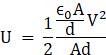
Here, V/d is the Electric intensity or Electric field so,


27