A spherical capacitor consists of two concentric spherical conductors, held in position by suitable insulating supports (Fig. 2.36). Show that the capacitance of a spherical capacitor is given by
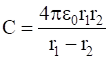
Where r1 and r2 are the radii of outer and inner spheres, respectively.
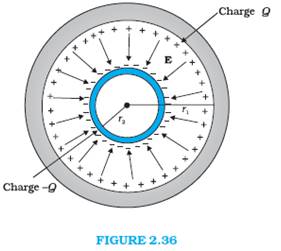
Radius of the outer shell = r1
Radius of the inner shell = r2
Charge on the inner surface of the outer shell = Q
Charge on the outer surface of the inner shell = -Q
Potential difference between the two shells, ![]()
![]()
Where, ![]() = Absolute Permittivity of free space = 8.85
= Absolute Permittivity of free space = 8.85![]() 10-12C2N-1m-2
10-12C2N-1m-2
Since, Capacitance, ![]()
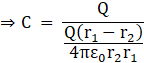
![]()
Hence, proved.
30