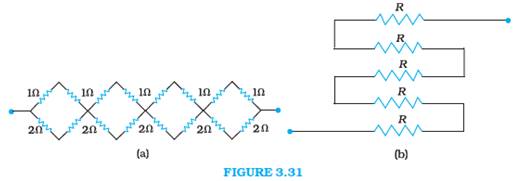
Determine the equivalent resistance of networks shown in Fig. 3.31.
(a) 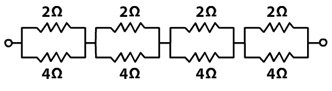
It can be observed from the given circuit that in the first small loop, two resistors
of resistance 1 Ω each are connected in series.
Hence, their equivalent resistance = (1 + 1) = 2 Ω
It can also be observed that two resistors of resistance 2 Ω each are connected in series.
Hence, their equivalent resistance = (2 + 2) = 4 Ω.
Now the given circuit diagram can be explained as
Now draw 4 loops each having 2 resistors of 2 Ω and 4 Ω connected in parallel.
Hence Equivalent Resistance Re of each loop is ![]()
⇒ Re = 4/3 Ω
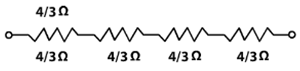
Since all 4 loops will be connected in series and each loop will have 4/3 Ω resistance
Hence, equivalent resistance of the given circuit is 4 × 4/3 = 16/3 Ω .
(b) ![]()
From the given circuit that five resistors of resistance R each are connected in series.
Hence, equivalent resistance of the circuit = R + R + R + R + R = 5R