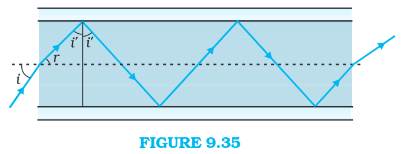
Given:

(a) Refractive index of the glass fibre,

Refractive index of the outer covering of the pipe, μ₂ = 1.44
Angle of incidence = i°
Angle of refraction = r°
Angle of incidence at the interface = i^’
The refractive index (μ) of the core interface is given as:

μ = …(1)

Where,

�₂ = refractive index of outer covering

�₁ = refractive index of inner covering

i^’ = angle of incidence at interface

From equation (1)

sin i^’ = �₁/ �₂

⇒ sin i^’ = 1.44/1.68

⇒ i^' = 59°

For the critical angle, total internal reflection takes place only when i > i’,

i.e., i > 59°
Maximum angle of reflection,

r_max = 90°−i′

⇒ r_max = 90°−59° = 31°
Let, imax be the maximum angle of incidence.
The refractive index at the air − glass interface, μ₁ = 1.68

⇒

⇒ sin i_max = �₁ × sin r_max

sin i_max = 1.68 × 0.5150 = 0.8652

Therefore i_max = sin^-1(0.86)

i_max = 60°

Thus, all the rays incident at angles lying in the range 0 < i < 60° will suffer total internal reflection.

(b) If the outer covering of the pipe is not present, then:
Refractive index of the outer pipe, μ1 = Refractive index of air = 1
For the angle of incidence i = 90°, we can write Snell’s law at the air − pipe interface as:
sin i /sin r = μ

Where,

i = angle of incidence

r = angle of refraction

sin i/ sin r = 1.68

sinr = sin90°/1.68

Sin r = 1/1.68

r = 36.5°

i^’ = 90° - r

⇒ i′ = 90°−36.5°

⇒ i^’ = 53.5°

Since i’ > r, all incident rays will suffer total internal reflection.