Two towers on top of two hills are 40 km apart. The line joining them passes 50 m above a hill halfway between the towers. What is the longest wavelength of radio waves, which can be sent between the towers without appreciable diffraction effects?
Fresnel’s distance is given by the relation, Zp = a2 / λ
Where,
λ is the wavelength of the radio waves
Zp is the Fresnel distance, which shows that on distance smaller than this, the spreading due to diffraction smaller compared to the size of the beam.
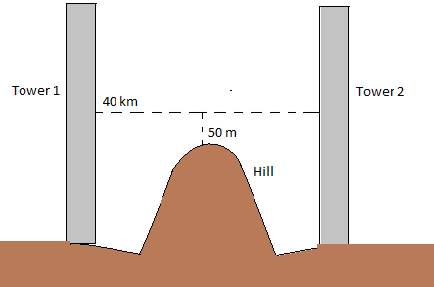
If we want to prevent diffraction of the radio waves , According to the validity of ray optics, the distance of the middle should be less than The size of aperture “a” = 50 m
Z= 20 km = d/2 = 2 × 104 m
Aperture can be taken as:
a = 50 m
The longest wavelength of radio waves which can be sent without any hindrance due to diffraction effect,
λ = a2 / Zp
⇒ ![]()
⇒ λ = 1250 × 10 - 4 m = 12.5 cm
Therefore, the longest wavelength of the radio waves is 12.5 cm