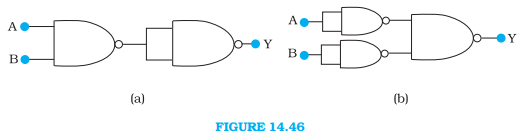
The circuit (a) is as follows:

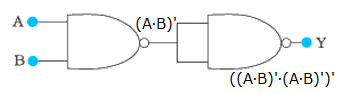
The first NAND gate gives the output (A∙B)’. The second NAND gate gives the output ((A∙B)’∙(A∙B)’)’.

Using De Morgan’s law,

((A∙B)’∙(A∙B)’)’ = ((A∙B)’)’ + ((A∙B)’)’ = (A∙B) + (A∙B) = A∙B (Since, A + A = A)

So, the output is Y = A∙B. The circuit acts as an AND gate.

The truth table for the circuit is as follows:

The circuit (b) is as follows:

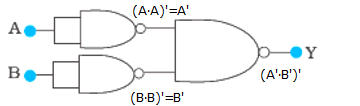
The first NAND gate gives (A∙A)’ = A’ as the output. The second NAND gate gives (B∙B)’ = B’ as the output. The last NAND gate gives (A’∙B’)’ as the output.

Using De Morgan’s law,

(A’∙B’)’ = (A’)’ + (B’)’ = A + B

So, the output is A + B. The circuit acts as an OR gate.

The truth table for the circuit is as follows:

NOTE: NAND gate is a universal gate because it can be used to implement any Boolean function without using any other gates.