Given:

Magnetic field strength, B = 1.5 T

Radius of cylinder, r = 10 cm

Current in wire travelling north to south, I = 7A

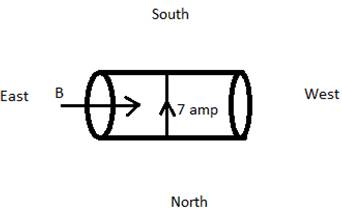
(a) Let the force on wire = F₁

If the wire intersects the axis of the magnetic field, then we observe that length of wire will be equal to the diameter of the cylinder.

L₁ = 2 × r = 20 cm

We know that,

F = B × I × L₁ × sinθ …(1)

Where,

F = Force on wire

B = magnetic field strength

I = current through the wire

L₁ = length of wire

θ = angle between direction of field and direction of current

Since, the field is along east to west and current flows along north south, direction so, θ = 90°.

By putting the values of B, I and L₁ in equation 1.

⇒ F = 1.5T × 7A × 0.2m × sin90°

⇒ F = 2.1 N

So, force on wire is 2.1 N and it acts in vertically downward direction.

(b) Let the force on wire = F₂

If the wire is turned towards Northeast-Northwest direction.

We observe that wire has been turned 45°, i.e. θ = 45°

L₂ = L₁/sinθ.

L₂ = 2 × L₁

F₂ = B × I × L₂ × sinθ

F₂ = B × I × L₂

F₂ = 2.1 N

Hence the force is 2.1 N and it acts vertically downwards.

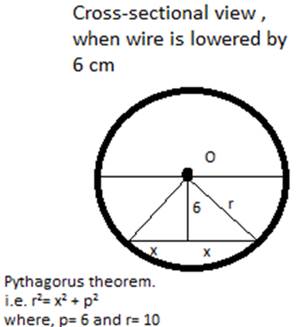
(c) Let, the force on wire = F₃

The wire has been lowered 6 cm,

⇒ x = ( r²-p²)^0.5

⇒ x = ( 100-36)^0.5

⇒ x = 8

So length of wire in the magnetic field region = 16 cm

(By using the geometry)

We know that,

F = B × I × L₁ × sinθ …(1)

Now, putting the values in B, T and I in equation 1.

⇒ F = 7T × 0.16A × 1.5T

⇒ F = 1.68 N

The direction of the force will be vertically downward, the direction of force is given by screw rule.