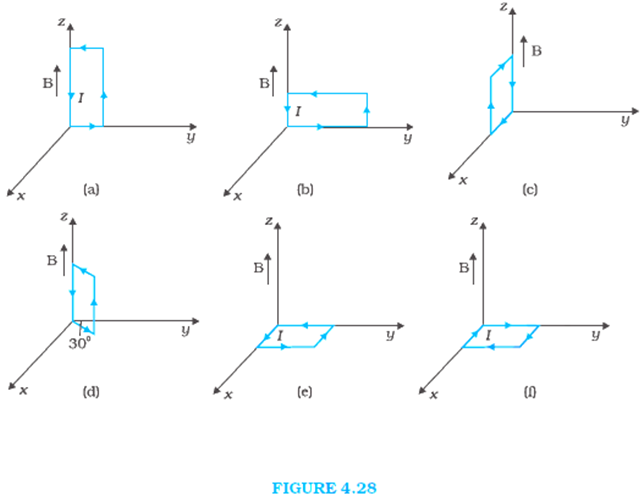
A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig. 4.28? What is the force on each case? Which case corresponds to stable equilibrium?

Question

Philoid · Accepted Answer

Given:

Magnetic field strength, B = 3000G

B = 3000 × 10^-4T

B = 0.3 T

Length of rectangular loop = 10 cm

Width of loop = 5 cm

Current in loop = 12 A

We know that,

Torque, T = IA × B …(1)

Where, I = current through loop

A = area of cross-section

B = magnetic field strength

Note: We take vector normal to the cross-section for A.

For each of the case we plug in the variables in equation (1).

(a) T = 12A × (50 × 10^-4) î m² × 0.3 T

= -1.8 × 10^-2 ĵ Nm (∵ î × = -ĵ )

Force on the loop is Zero as the angle between area of cross section and magnetic field is Zero.

(b) This case is similar to A, hence the results will also be same. There is no change in any vectors.

(c) T = IA × B

We observe that A is perpendicular to x-z plane and B is along z axis.

⇒ T = -12A × (50 × 10^-4)m² ĵ × 0.3T

⇒ T = -1.8 × 10^-2 î Nm (∵ ĵ × = -î )

(d) Magnitude of torque,

|T| = IA × B

⇒ |T| = 12 × (50 × 10^-4)m² × 0.3T

⇒ |T| = 1.8 × 10^-2 Nm

This torque is makes 240° with the positive x direction. The force again is Zero.

(e) T = IA × B

= 12 × (50 × 10^-4) m² × 0.3 T

= 0

Since cross section and magnetic field are in same direction net torque is zero. Net force is also Zero.

(f)

= 12 × (50 × 10^-4) × 0.3

= 0

Hence the torque and forces are zero.

Stable equilibrium:

In case E, the angle between A and B is zero. If we displace the wire, it will come back in this position, hence it is the stable equilibrium condition.

Unstable equilibrium:

In case F, the angle between A and B is 180°. If the wire is displaced, it will not come back in this position so we can conclude that it is the case for unstable equilibrium.