Figure 6.20 shows a metal rod PQ resting on the smooth rails AB and positioned between the poles of a permanent magnet. The rails, the rod, and the magnetic field are in three mutual perpendicular directions. A galvanometer G connects the rails through a switch K. Length of the rod = 15 cm, B = 0.50 T, resistance of the closed loop containing the rod = 9.0 mW. Assume the field to be uniform.
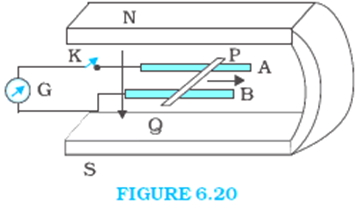
(a) Suppose K is open and the rod is moved with a speed of 12 cm s–1 in the direction shown. Give the polarity and magnitude of the induced emf.
(b) Is there an excess charge built up at the ends of the rods when K is open? What if K is closed?
(c) With K open and the rod moving uniformly, there is no net force on the electrons in the rod PQ even though they do experience magnetic force due to the motion of the rod. Explain.
(d) What is the retarding force on the rod when K is closed?
(e) How much power is required (by an external agent) to keep the rod moving at the same speed (=12cm s–1) when K is closed? How much power is required when K is open?
(f) How much power is dissipated as heat in the closed circuit? What is the source of this power?
(g) What is the induced emf in the moving rod if the magnetic field is parallel to the rails instead of being perpendicular?
Given: Length of the rod = 15 cm
Length of rod in metres l = 0.15 m
Magnetic field strength B = 0.50 T
Resistance of the loop R = 9 mΩ = 9 × 10 - 3 Ω
Emf induced in the loop = 9 mV
Speed of the rod, v= 12 cm/s
Speed of the rod in m/s, v= 0.12m/s
It is shown as below:

(a) Induced emf can be calculated as follows:
e = Bvl
e = 0.50T× 0.12ms-1× 0.15m
e = 9× 10-3V = 9mV
The polarity of the induced emf is such that the end P is positive and end Q is negative.
(b) Yes, there is an excess charge built up at the ends of the rods when K is open. When K is closed, the excess charge present will be maintained by the flow of current continuously.
(c) The net force on the rod PQ is zero still they experience magnetic force due to motion of the rod magnetic force is cancelled by the electric force set up. This happens because of the excess charge on both the opposite ends of the rod.
(d) The retarding force acting on the rod when K is closed can be calculated as follows:
F = iBl……………(i)
Where i= induced emf(e)/Resistance (RΩ)
I = 9mV/9×10-3Ω
I= 1A
Substituting the values in equation (i), we get
F = 1A× 0.50T× 0.15m
F = 75×10-3 N
(e) Power required when K is closed:
Power = Fv
P = 75×10-3 N× 0.12ms-1
P = 9×10 - 3 W
Power = 9 mW
When key K is open, there is no power required.
(f) Power dissipated H = I2R
H = 1A 2× 9×10-3Ω = 9 mW
9mW power is dissipated as heat in the closed circuit and the source of this power is external agent.
(g) The induced emf in the moving rod if the magnetic field is parallel to the rails instead of being perpendicular is zero because the motion of the rod doesn’t cross across the lines and therefore induced emf will be zero.