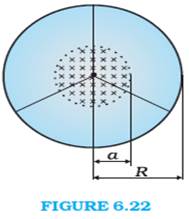
A line charge λ per unit length is lodged uniformly onto the rim of a wheel of mass M and radius R. The wheel has light non - conducting spokes and is free to rotate without friction about its axis (Fig. 6.22). A uniform magnetic field extends over a circular region within the rim. It is given by,

Question

A line charge λ per unit length is lodged uniformly onto the rim of a wheel of mass M and radius R. The wheel has light non - conducting spokes and is free to rotate without friction about its axis (Fig. 6.22). A uniform magnetic field extends over a circular region within the rim. It is given by, B = – B 0 k (r ≤ a; a < R) = 0 (otherwise) What is the angular velocity of the wheel after the field is suddenly switched off?

Philoid · Accepted Answer

Line charge per unit length is given by the following relation:

Total charge/ length = Q/2π r

Where r is the distance of the point within the wheel

Let m and R are mass and radius of the wheel

Magnetic field is given by the following relation:

The magnetic force at balanced by the centripetal force at a distance of r

i.e. BQv = mv²/r

v is the linear velocity of the wheel and is equal to v= 2π rλ

⇒ B × 2π rλ = mv/r

Or

As we know that angular velocity is given as: ω = v/r

⇒ w =

When R> a and r ≤ a

ω =