If sec θ + tan θ = p, prove that
(i) 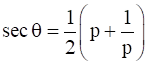
(ii) 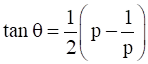
(iii) 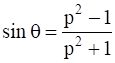
(i) Given: sec θ + tan θ = p ……(1)
Then, (sec θ + tan θ) × ![]() = p
= p
⇒ ![]() = p
= p
⇒ ![]() = p
= p
⇒ sec θ – tan θ = (1/p) ……(2)
Adding equation (1) and (2), we get:
2 sec θ = p + (1/p)
⇒ sec θ = ![]()
Therefore, sec θ = ![]()
(ii) Given: sec θ + tan θ = p ……(1)
Then, (sec θ + tan θ) × ![]() = p
= p
⇒ ![]() = p
= p
⇒ ![]() = p
= p
⇒ sec θ – tan θ = (1/p) ……(2)
Subtracting equation (2) from (1), we get:
2tan θ = p – (1/p)
⇒ tan θ = ![]()
(iii) Since sin θ = tan θ/sec θ
= 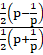
= 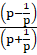
= ![]()
13