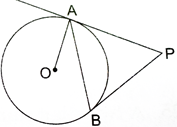
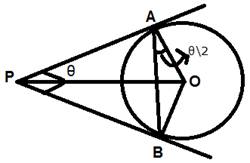
fig.11

Let ∠ APB = θ

In Δ APB,

PA = PB

[∵ Tangents drawn from an exterior point to the circle are equal in length]

⇒ Δ APB is an isoceles triangle.

∴ ∠ PAB = ∠ PBA = α [LET]

Now,

∠ APB + ∠ PAB + ∠ PBA = 180° [∵ sum of all the angles of Δ=180°]

⇒ θ + α + α = 180°

⇒ 2α = 180° – θ

∴ α = ∠ PAB = 90° – (θ/2)

Also, OA⊥AP

[∵ radius of a circle is always ⊥ to the tangent at the point of contact.]

∴ ∠ PAB + ∠ OAB = 90°

⇒ 90° – (θ/2) + ∠ OAB = 90°

⇒ ∠ OAB = (θ/2) = (1/2)∠ APB

∴ ∠ APB = 2 ∠ OAB

Hence, Proved.