Show that the relation R in the set R of real numbers, defined as R = {(a, b) : a ≤ b 2 } is neither reflexive nor symmetric nor transitive.

Question

Philoid · Accepted Answer

It is given that R = {(a, b) : a ≤ b²}

We can see that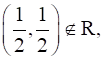

Since,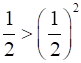

Therefore, R is not reflexive.

Now, (1,4) ϵ R as 1 < 4²

But 4 is not less than 1².

Then, (4,1) ∉ R

Therefore, R is not symmetric.

Now, (3, 2), (2, 1.5) ϵ R

But, 3 > (1.5)² = 2.25.

Then, (3, 1.5) ∉ R

Therefore, R is not transitive.

Therefore, R is neither reflexive, nor symmetric, nor transitive.