Show that the function f : R* → R* defined by 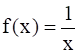is one-one and onto, where R* is the set of all non-zero real numbers. Is the result true, if the domain R* is replaced by N with co-domain being same as R*?

Question

Philoid · Accepted Answer

It is given that f : R* → R* defined by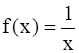

f(x) = f(y)

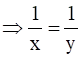
⇒ x = y

⇒ f is one – one.

We can see that y ϵ R, there exists 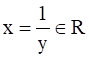, such that

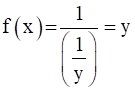
⇒ f is onto.

Therefore, function f is one-one and onto.

Now, Let us consider g: N → R_* defined by

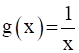
Then, we get,

g(x₁) = g(x₂)

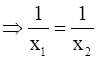
⇒ x₁ = x₂

⇒ g is one–one.

It can be observed that g is not onto as for 1.2 ϵ R there does not exist any x in N such that

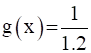
Therefore, function g is one –one but not onto.