In each of the following cases, state whether the function is one-one, onto or bijective. Justify your answer.

Question

In each of the following cases, state whether the function is one-one, onto or bijective. Justify your answer. f : R → R defined by f (x) = 3 – 4x

Philoid · Accepted Answer

It is given that f : R → R defined by f (x) = 3 – 4x

Let x₁, x₂ϵ R such that f(x₁) = f(x₂)

⇒ 3 – 4x₁ = 3 – 4x₂

⇒ -4x₁ = -4x₂

⇒ x₁ = x₂

⇒ f is one- one

For any real number (y) in R, there exist 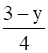in R such that

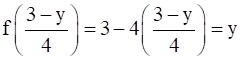
⇒ f is onto.

Therefore, function f is bijective.