Let f : N → N be defined by
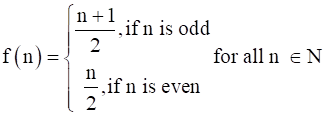
State whether the function f is bijective. Justify your answer.
It is given that
f : N → N be defined by
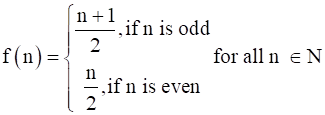
We can observed that:
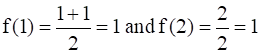 (by using the definition of f)
(by using the definition of f)
Thus, f(1) = f(2), where 1 ≠ 2.
Therefore, f is not one-one.
Now, let us consider a natural number (n) in co domain N.
Case I: When n is odd.
Then, n = 2r +1 for some r ϵ N.
⇒ there exist 4r + 1 ϵ N such that f(4r+1) = 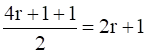
Case II: When n is even.
Then, n = 2r for some r ϵ N.
⇒ there exist 4r ϵ N such that f(4r) = 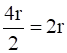
Therefore, f is onto.
⇒ Function f is not one-one but it is onto.
Thus, Function f is not bijective function.
14