Let A = R – {3} and B = R – {1}. Consider the function f: A → B defined by 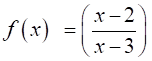 . Is f one-one and onto? Justify your answer.
. Is f one-one and onto? Justify your answer.
It is given that A = R – {3} and B = R – {1}
f: A → B defined by

Now, let x, y ϵ A such that f(x) = f(y)

⇒ (x-2)(y-3) = (y-2)(x-3)
⇒ xy – 3x -2y + 6 = xy -3y -2x +6
⇒ -3x -2y = -3y -2x
⇒ x = y
⇒ f is one –one.
Let y ϵ B = R – {1}
Then, y ≠ 1.
The function f is onto if there exist x ϵ A such that f(x) = y
Now, f(x) = y

⇒ x – 2 = xy -3y
⇒ x(1-y) = -3y + 2

⇒ y ϵ B, there exists  ϵ A such that
ϵ A such that

⇒ f is onto.
Therefore, function f is one- one and onto.
14