It is given that f: R → R be defined as f (x) = 3x.

Let x, y ϵ R such that f(x) = f(y).

⇒ 3x = 3y

⇒ x = y

⇒ f is one–one.

Also, for any real number (y) in co–domain R, there exists 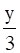in R such that

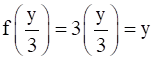
Therefore, f is onto.

Therefore, function f is one-one and onto.