Consider f : R → R given by f (x) = 4x + 3. Show that f is invertible. Find the inverse of f.
It is given that f : R → R given by f (x) = 4x + 3
Let f(x) = f(y)
⇒ 4x +3 = 4y +3
⇒ 4x = 4y
⇒ x = y
⇒ f is one- one function.
Now, for y ϵ R, Let y = 4x +3
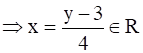
⇒ for any y ϵ R, there exists x = 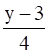 ϵ R
ϵ R
such that, f(x) = 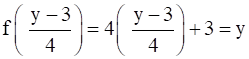
⇒ F is onto function.
Since, f is one –one and onto
⇒ f-1 exists.
Let us define g: R → R by g(x) = 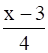
Now, (gof)(x) = g(f(x)) = g(4x + 3) = 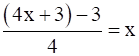
(fog)(y) = f(g(xy)) = 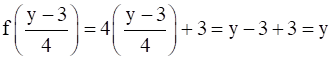
Therefore, gof = fog = IR
Therefore, f is invertible and the inverse of f is given by
f-1 (y) = g(y) = 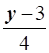 .
.
7