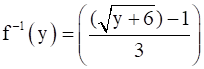
It is given that f: R+ → [–5, ∞) given by f(x) = 9x² + 6x – 5.

Let y be any element of [-5, ∞)

Now, let y = 9x² + 6x – 5

⇒ y = (3x+1)² -1-5 = (3x+1)2 – 6

⇒ 3x + 1 =

⇒ f is onto and it’s range is f = [-5, ∞)

Now, Let us define g: [-5, ∞) → R₊ as g(y) =

Now, we have:

(gof)(x) = g(f(x)) = g(9x² + 6x – 5)

= g((3x+1)² – 6)

And, (fog)(y) = f(g(y)) =

Thus, gof = I_R anf fog = I(-5, ∞)

Therefore, f is invertible and the inverse of f is given by