For each operation ∗ defined below, determine whether ∗ is binary, commutative or associative.

Question

For each operation ∗ defined below, determine whether ∗ is binary, commutative or associative. On Q, define a ∗ b =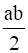

Philoid · Accepted Answer

It is given that On Q, define a ∗ b =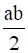

Now, 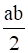ϵ Q, so the operation * is binary.

We know that ab = ba for a,b ϵ Q

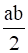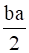⇒ = for a, b ϵ Q

⇒ a * b = a * b for a,b ϵ Q

⇒ The operation * is commutative.

Also for all a,b,c ϵ Q, we get,

(a * b) * c = (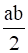) * c =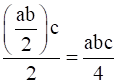

a * (b * c) = a * () =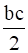

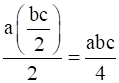
⇒ (a * b) * c = a * (b * c)

⇒ the operation * is associative.