For each operation ∗ defined below, determine whether ∗ is binary, commutative or associative.

Question

For each operation ∗ defined below, determine whether ∗ is binary, commutative or associative. On R – {–1}, define a ∗ b =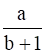

Philoid · Accepted Answer

It is given that On R, * – {– 1}, define a ∗ b =

ϵ R for b ≠ -1, so the operation * is binary.

We can see that 1 * 2 = and 2 * 1=

⇒ 1 * 2 ≠ 2 * 1; where 1,2 ϵ R – {-1}

⇒ the operation * is not commutative.

Now, we can observed that

(1 * 2) * 3 =

1 * (2 * 3) = 1 *

⇒ (1 * 2) * 3 ≠ 1 * (2 * 3), where 1,2,3 ϵ R * – {– 1}

⇒ The operation * is not associative.