Let ∗ be a binary operation on the set Q of rational numbers as follows: a ∗ b =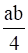 Find which of the binary operations are commutative and which are associative.

Question

Philoid · Accepted Answer

It is given that ∗ be a binary operation on the set Q of rational numbers is defined as

a ∗ b =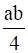

For a, b ϵ Q, we get,

a * b = 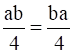= b * a

⇒ the operation is commutative.

For a, b, c ϵ Q, we get,

(a * b) * c =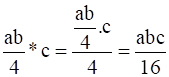

a * (b * c) = a *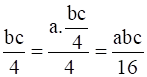

⇒ (a * b) * c = a * (b * c)

Therefore, the operation * is associative.

Let ∗ be a binary operation on the set Q of rational numbers as follows:a ∗ b =Find which of the binary operations are commutative and which are associative.

Let ∗ be a binary operation on the set Q of rational numbers as follows:
a ∗ b =

Find which of the binary operations are commutative and which are associative.