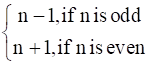It is given that f : W → W be defined as

f(n) =

Let f(n) = f(m)

We can see that if n is odd and m is even, then we will have n -1 = m +1.

⇒ n – m = 2

⇒ this is impossible

Similarly, the possibility of n being even and m being odd can also be ignored under a similar argument.

Therefore, both n and m must be either odd or even.

Now, if both n and m are odd, then we get:

f(n) = f(m)

⇒ n -1 = m -1

⇒ n = m

Again, if both n and m are even, the we get:

f(n) = f(m)

⇒ n +1 = m + 1

⇒ n = m

⇒ f is one – one.

Now, it is clear that any odd number 2r + 1 in co-domain N is the image of 2r in domain N and any even number 2r in co – domain N is the image of 2r +1 in domain N.

⇒ f is onto.

⇒ f is an invertible function.

Now, let us define g : W → W be defined as

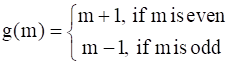
Now, when n is odd:

gof(n) = g(f(n)) = g (n-1) = n -1 +1 = n (when n is odd, then n-1 is even)

And when n is even:

gof(n) = g(f(n)) = g (n+1) = n +1 -1 = n (when n is even, then n+1 is odd)

Similarly, when m is odd:

fog(m) = f(g(m)) = f (m-1) = m -1 +1 = m

And when n is even:

fog(m) = f(g(m)) = f (m+1) = m +1 -1 = m

Therefore, gof = I_W and fog = I_W

Therefore, f is invertible and the inverse of f is given by f^-1 = g, which is the same as f.

Thus, the inverse of f is f itself.