Show that the function f: R → {x ∈ R : – 1 < x < 1} defined by 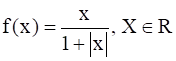 is one-one and onto function.
is one-one and onto function.
It is given that f: R → {x ∈ R : – 1 < x < 1} defined by  , x ∈ R
, x ∈ R
Now, suppose that f(x) = f(y), where x,y ϵ R.

We can see that if x is positive and y is negative, then we get:

Since, x is positive, and y is negative.
Then, 2xy ≠ x –y.
Thus, the case of x being positive and y being negative can be ruled out.
Similarly, x being negative and y being positive can also be ruled out.
Therefore, x and y have to be either positive or negative.
When x and y are both positive, we get:
f(x) = f(y)

And when x and y are both negative, we get:
f(x) = f(y)

⇒ f is one- one.
Now, let y ϵ R such that -1 < y < 1.
It y is negative, then there exists  such that
such that

⇒ f is onto.
Therefore, f is one – one and onto.