Give examples of two functions f: N → N and g : N → N such that g o f is onto but f is not onto.

Question

Give examples of two functions f: N → N and g : N → N such that g o f is onto but f is not onto. (Hint: Consider f (x) = x + 1 and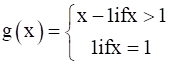

Philoid · Accepted Answer

It is given that f: N → N by, f(x) = x + 1

And, g : N → N by,

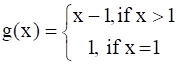
Now, consider element 1 in co-domain N. So, it is clear that this element is not an image of any of the elements in domain N.

⇒ f is onto.

Now, gof: N → N is defined as:

gof(x) = g(f(x)) = g(x+1) = (x + 1) – 1 [x ϵ N = > (x+1) > 1]

Then we can see that for y ϵ N, there exists x = y ϵ N such that gof(x) = y.

Therefore, gof is onto.