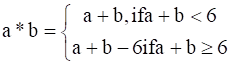
Define a binary operation ∗ on the set {0, 1, 2, 3, 4, 5} as Show that zero is the identity for this operation and each element a ≠ 0 of the set is invertible with 6 – a being the inverse of a.

Question

Philoid · Accepted Answer

Let X = {0, 1, 2, 3, 4, 5}

The operation * on X is defined as

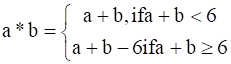
An element e ϵ X is the identity element for the operation *,

If a * e = a = e * a a ϵ X.

For a ϵ X, we can see that:

a * 0 = a + 0 = a [a ϵ X = > a + 0 < 6]

0 * A = 0 + a = a [a ϵ X = > a + 0 < 6]

⇒ a * 0 = a = 0 * a a ϵ X.

Therefore, o is the identity element for the given operation *.

An element a ϵ X is invertible if there exists b ϵ X such that

a * b = 0 = b * a.

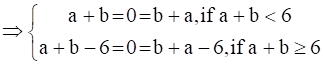
a = -b or b = 6 – a

But, X = {0, 1, 2, 3, 4, 5} and a, b ϵ X. Then, a ≠ -b.

Therefore, b = 6 – a is the inverse of a ϵ X.

Thus, the inverse of an element a ϵ X, a ≠ 0 is 6 – a, a^-1 = 6 – a.

Define a binary operation ∗ on the set {0, 1, 2, 3, 4, 5} asShow that zero is the identity for this operation and each element a ≠ 0 of the set is invertible with 6 – a being the inverse of a.

Define a binary operation ∗ on the set {0, 1, 2, 3, 4, 5} as

Show that zero is the identity for this operation and each element a ≠ 0 of the set is invertible with 6 – a being the inverse of a.