Let A = {–1, 0, 1, 2}, B = {–4, –2, 0, 2} and f, g: A → B be functions defined by f (x) = x 2 – x, x ∈ A and 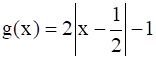, x ∈ A. Are f and g equal? Justify your answer. (Hint: One may note that two functions f: A → B and g: A → B such that f (a) = g(a) ∀ a ∈ A, are called equal functions).

Question

Philoid · Accepted Answer

It is given that A = {–1, 0, 1, 2}, B = {– 4, – 2, 0, 2}

And also, it is given that f, g: A → B be functions defined by f (x) = x² – x, x ∈ A and 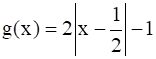, x ∈ A

We can see that

f(-1) = (-1)² – (-1) = 1 + 1 = 2

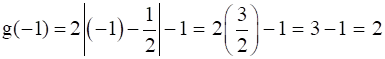
⇒ f(-1) = g(-1)

f(0) = (0)² – 0 = 0 + 0 = 0

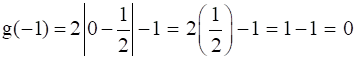
⇒ f(0) = g(0)

f(1) = (1)² – 1 = 1- 1 = 0

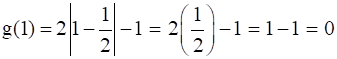
⇒ f(1) = g(1)

f(2) = (2)² – 2 = 4- 2 = 2

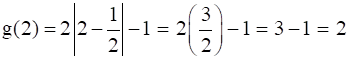
f(2) = g(2)

Thus, f(a) = g(a) . a ϵ A

Therefore, the functions f and g are equal.

Let A = {–1, 0, 1, 2}, B = {–4, –2, 0, 2} and f, g: A → B be functions defined by f (x) = x2 – x, x ∈ A and , x ∈ A. Are f and g equal?Justify your answer. (Hint: One may note that two functions f: A → B and g: A → B such that f (a) = g(a) ∀ a ∈ A, are called equal functions).