Is the function defined by
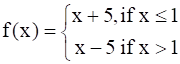
a continuous function?
The given function is ![]()
The function f is defined at all points of the real line.
Let k be the point on a real line.
Then, we have 3 cases i.e., k < 1, or k = 1 or k > 1
Now,
Case I: k < 1
Then, f(k) = k + 5
![]() = k + 5 = f(k)
= k + 5 = f(k)
Thus, ![]()
Hence, f is continuous at all real number less than 1.
Case II: k = 1
Then, f(k) = f(1) = 1 + 5 = 6
![]() = 1 + 5 = 6
= 1 + 5 = 6
![]() = 1 - 5 = -4
= 1 - 5 = -4
![]()
Hence, f is not continuous at x = 1.
Case III: k > 1
Then, f(k) = k -5
![]() = k - 5
= k - 5
Thus, ![]()
Hence, f is continuous at all real number greater than 1.
Therefore, x = 1 is the only point of discontinuity of f.
13