Find the values of a and b such that the function defined by
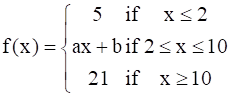 is a continuous function.
is a continuous function.
It is given function is 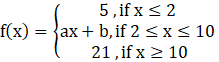
We know that the given function f is defined at all points of the real line.
Thus, f is continuous at x = 2, we get,
![]()
⇒ ![]()
⇒ 5 = 2a + b = 5
⇒ 2a + b = 5………………(1)
Thus, f is continuous at x = 10, we get,
![]()
⇒ ![]()
⇒ 10a + b = 21 =21
⇒ 10a + b = 21………………(2)
On subtracting eq. (1) from eq. (2), we get,
8a = 16
⇒ a = 2
Thus, putting a = 2 in eq. (1), we get,
2 × 2 + b = 5
⇒ 4 + b = 5
⇒ b = 1
Therefore, the values of a and b for which f is a continuous function are 2 and 1 resp.
30