Show that the matrix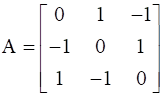 is a skew symmetric matrix.
is a skew symmetric matrix.
A matrix is said to be skew symmetric if the transpose of the matrix is equal to the negative of the matrix. This means that A’ = -A.
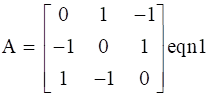
Now, we know that the transpose of matrix A is
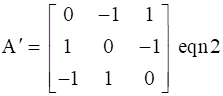
Now if we carefully look at the equation 2 we can rewrite it as
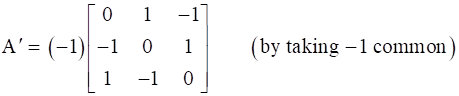
So, A’ = (-1) × A (from equation 1)
⇒ A’ = -A, hence we can say that Matrix A is a skew symmetric matrix.
Hence proved
9