For the matrix 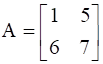 , verify that
, verify that
(A – A’) is a skew symmetric matrix
(A – A’) is a skew symmetric matrix.
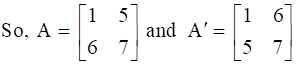 .
.
subtracting A’ from A, we get,
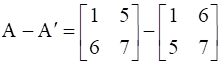
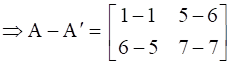
Explanation: Now to show that the matrix obtained i.e. (A + A’) is skew symmetric we need to calculate its transpose and prove that the matrix (A + A’) is equal to the negative of its transpose are equal. This means that (A + A’) = -(A + A’)’.
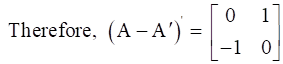
We can rewrite above equation as
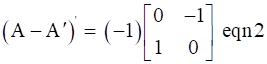
Also, (A – A’)’ = (-1) × (A – A’) (from equation 1)
(A – A’)’ = -(A – A’), hence we can say that Matrix A is a skew symmetric matrix.
Hence proved.
8