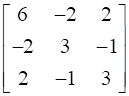
As per Theorem 2 “Any square matrix can be expressed as the sum of a symmetric and skew symmetric matrix.” So in order to prove this we will be using Theorem 1 which states that “For any square matrix A with real number entries, A + A’ is a symmetric matrix and A – A’ is a skew symmetric matrix.”

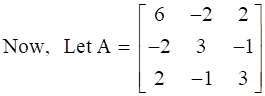
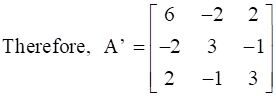
Now, on adding A and A’ we will get,

.

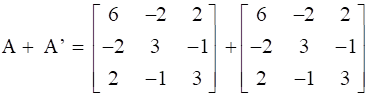
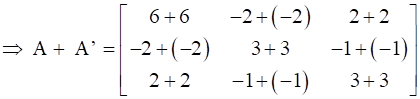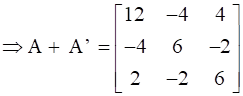
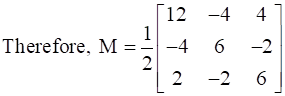
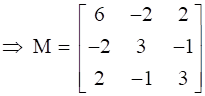
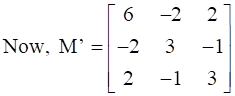
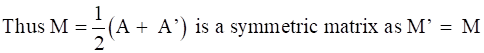
Now, on subtracting A’ from A we will get,

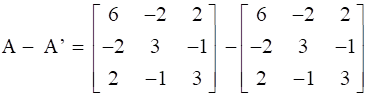
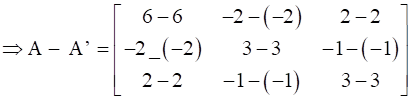
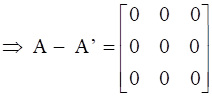
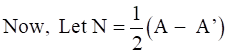
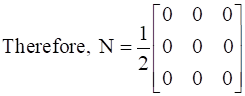
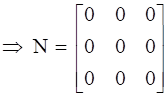
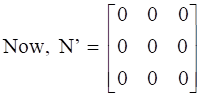
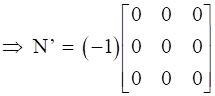
⇒ N’ = -N

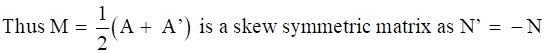
Now, Add M and N, we get,

.

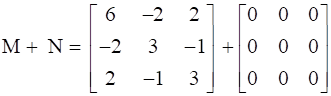
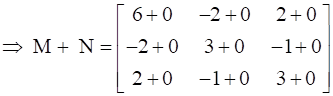
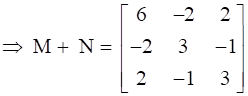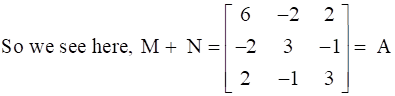
Thus, A is represented as the sum of a symmetric matrix M and a skew symmetric matrix N.