Using elementary transformations, find the inverse of each of the matrices.
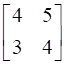
First of all we need to check whether the matrix is invertible or not. For that-
For the inverse of a matrix A to exist,
Determinant of A ≠ 0
Here ∣A∣ = (4)(4) – (5)(3) = 1
So the matrix is invertible.
Now to find the inverse of the matrix,
We know AA-1 = I
Let’s make augmented matrix-
→ [ A : I ]
→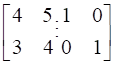
Apply row operation- 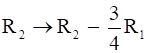
→ 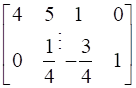
Apply row operation- R1→ R1/4
→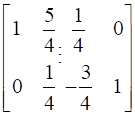
Apply row operation- R1→ R1 - 5R2
→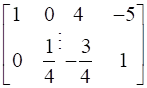
Apply row operation- R2→ 4R2
→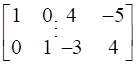
The matrix so obtained is of the form –
→ [ I : A-1 ]
Hence inverse of the given matrix -
→ 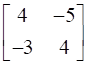
9